3D printed fractals at JMU 3SPACE

The James Madison University 3SPACE classroom kicked off the Fall 2017 semester with ten new 3D printers incorporated into our classroom stations: five Ultimaker 2+ printers, and five Ultimaker 3 printers.

This new equipment enabled us to increase our capacity to 24 students and to offer courses that require more challenging print jobs, which made it possible for us to offer two new 3-credit general education courses: MATH 103 - The Nature of Mathematics and ART 300E - 3D Printing and the Creative Community. In these courses, we’ll be exploring fractals, four-dimensional representations of objects, extreme remixes, and everything our students can dream up!

In this article, we’ll talk about how we implemented the first unit in the MATH 103 course: exploring fractals. For information on all of our JMU 3SPACE courses and workshops, see the 3SPACE website.

First fractal prints

The 3SPACE classroom is not part of our university Engineering or Design departments; we serve the general university community. This means that the students that come to us typically have no 3D printing or design experience. In the case of MATH 103, which satisfies the JMU general education math requirement for non-majors, our students also don’t know much math. In fact, most of them will freely volunteer that they don’t like math at all! So, we started slow, having students find fractals on Thingiverse to download and print.

The purpose of this assignment was to help students become familiar with fractals and fractal properties, and to train them to use the 3D printers. A secondary goal was to have students participate in the online 3D printing community; they use the community to find designs, and then they give back to the community by documenting their prints on our public class Wordpress blog, in the First Fractal section.

While students printed and documented their first fractals, we spent class time discussing exactly what makes something a fractal, and what fractal properties were illustrated by each of their printed fractals. Students also started reading Falconer’s book Fractals: A Very Short Introduction. We also watched some YouTube videos on fractals, including this excellent Numberphile video on the Dragon Curve:

Here are some of the great fractal models that our math students found to print: A Nautilus shell, a Pythagorous tree, and a Vicsek fractal cross.

Student-designed fractals

The next fractal assignment for MATH 103 was for students to design their own, brand-new fractals. We gave the students a brief introduction to Tinkercad and then let them struggle to produce something that they felt had fractal properties. We purposely didn’t give them much direction here, in the hopes that the students would really have to think hard about “what makes a fractal a fractal”.

The students came up with some very interesting things! Here are three of them. First, a simple Whirly Cross Fractal that gets smaller and smaller as you go to the inside:

Second, a beautiful self-intersecting Pyramid Spiral Fractal that twists in on itself (this one is courtesy of “Control-D” in Tinkercad):

And third, a Mandala Fractal where each ring is ⅘ of the size of the one outside it:

Perimeter, area, and volume

Eventually, we had to buckle down and do some calculations. We discussed in class how various fractals might have infinite perimeter but finite area, or infinite surface area but finite volume. A good starting point for this topic is Randy Dobson’s video on the Koch snowflake:

Students attempted to compute perimeter, area, or volume of their new fractal creations, but were permitted to fall back to doing computations on one of their earlier “First Fractals” if necessary. (The complexity and self-intersections of some of the students’ original creations sometimes made it too difficult to do these calculations.)

Here is some student work finding the area of Level 2 of the Pythagorean fractal pictured earlier:

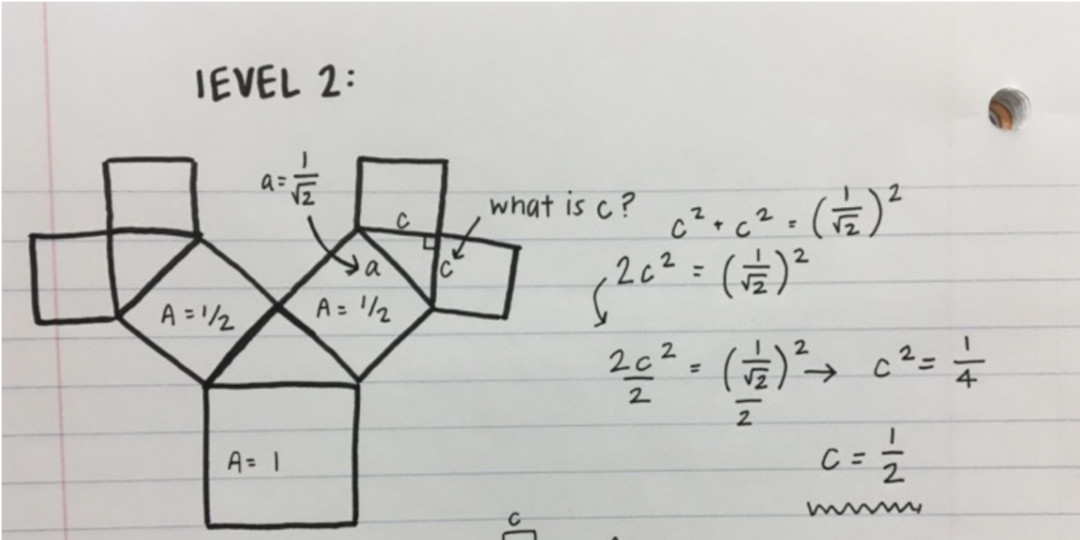
During class, we talked a bit about geometric series and what the behavior of these fractal measurements after infinitely many iterations. Since our MATH 103 students come from many different backgrounds and most of them have not had calculus before, the challenge as an instructor is to pick out just that one piece of math that students need, and to try to put it into context. Nearly all of the students’ fractal calculations ended up being related to geometric series, so we focused on understanding finite and infinite geometric series. Pretty much everything boiled down to understanding the following:

Dimension

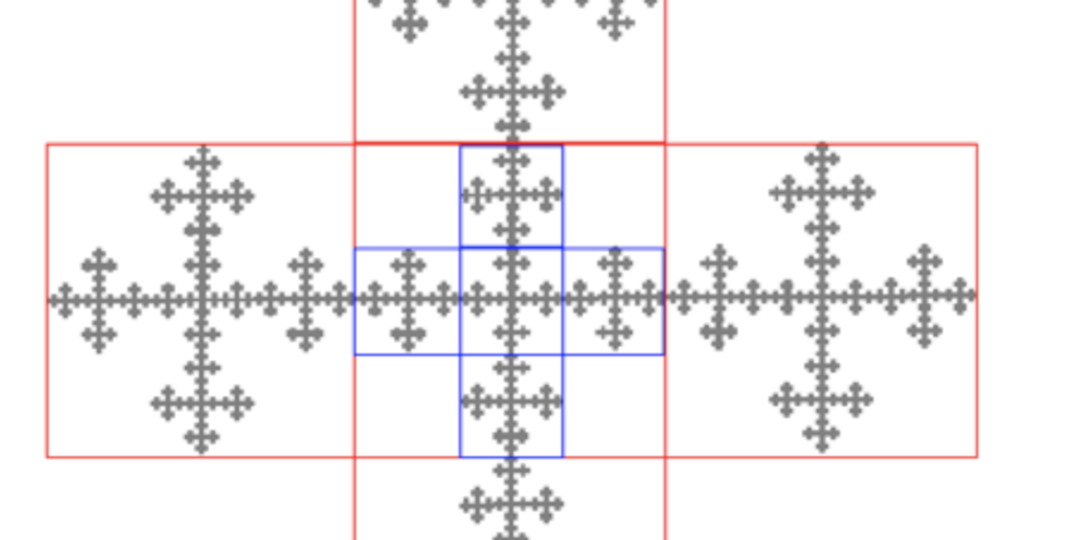
The final step in our fractal exploration was to think about fractal dimension. Fractal dimension can be difficult to calculate, but it is easy for certain types of self-similar fractals. We used the method explained in the first half of the excellent video Fractals Are Typically Not Self-Similar from 3Blue1Brown.

With this method, students identify a linear scaling factor that shrinks the self-similar fractal onto an exact copy of itself, and then count how many of those smaller copies it takes to make up the entire fractal.  Then they use the formula (1/scaling)^D = 1/(number of copies) and use logarithms to solve for D. Here is an example of a student calculation, for the dimension of the Vicsek fractal pictured earlier:

What’s next?

We’re still just six or seven weeks into the semester, so we have lots of time to explore new mathematical objects with 3D printing. We just started our second unit, where students choose interesting topics from Matt Parker’s book Things To Make and Do in the Fourth Dimension and then design and print 3D models that illustrate those topics. Students have chosen topics ranging from Prince Rupert’s Cube and the Reuleaux Tetrahedron to Trefoil Knots and the Borromean Rings. You can see all of their projects-in-progress at the Open Projects category on our class blog.